Merge Two Lists - Iterative & Recursive Solutions

April 21, 2022
|
Algorithms

This is LeetCode problem #21. I liked it so much that I wanted to write a post with an in depth walkthrough of the logic to solve it both iteratively & recursively.

Here’s the problem - you’re given two linked lists that are guaranteed to have values in ascending order. We need to combine these two lists into a single list with values in ascending order. Here’s a visual to help demonstrate what we want to achieve:

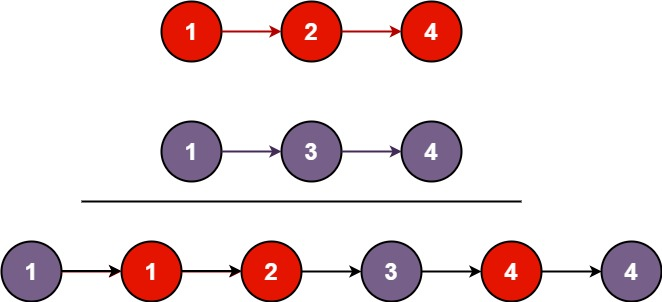
As you can see, we can’t just insert one linked list into the other, since we may need to alternate between values from one list and the other several times. This rules out a binary search algorithm 😢. We will need to build a result list by comparing the values from both lists. If you need a refresher on singly linked lists, here is a good resource to read. Basically, we have to access one element at a time, starting at the beginning of the list. Each element has a value and points to the next value (looking at any single element, we have no idea what element came before or if there even was a preceding element - we just know the current element’s value and the next element, if there is one).

The first approach is iterative - we compare the values of the first elements from both lists, appending the smaller value to our result list & then comparing again. By the end we’ll have a sorted linked list. Here’s the code:


class Solution {
    func mergeTwoLists(_ list1: ListNode?, _ list2: ListNode?) -> ListNode? {
        
        // Iterative
        
        // If a list is empty, return the other list.
		// The other list may be empty as well, but that won't break anything.
		// If we have only one list we can just return it as the sorted list, since the input lists are guaranteed to be sorted.
        guard let list1 = list1 else { return list2 }
        guard let list2 = list2 else { return list1 }
        
        // We need to hold a reference to the first node of our result list, so we can return it at the end.
        // We also need to keep track of the last node in our list, so we can append the next node as needed.
        var result: ListNode?
        var resultLastNode: ListNode?
        
        // These variables are pointers to our current node in each list.
        var l1NodeOptional: ListNode? = list1
        var l2NodeOptional: ListNode? = list2
        
        // This helper function reduces the amount of repeated logic later.
        // Essentially we need to check if we already have a result node,
        // although it checks that we have a `lastNode`, because of the logic
        // we know that a non nil `lastNode` also means we have a non nil `result` node.
        func append(_ node: ListNode?) {
            guard let node = node else { return }
            
            if let lastNode = resultLastNode {
                lastNode.next = node
                resultLastNode = node
            } else {   
                result = node
                resultLastNode = node
            }
        }
        
        // Now we start combining the two lists.
        // Start iterating through list 1 nodes and comparing to list 2 nodes.
        while let l1Node = l1NodeOptional {
            if let l2Node = l2NodeOptional {
                // We haven't reached the end of either list, compare the values and append the smaller one to our result.
                // Then move the pointer of the list with the smaller value to the next value.
                if l1Node.val < l2Node.val {
                    append(l1Node)
                    l1NodeOptional = l1Node.next
                } else {
                    append(l2Node)
                    l2NodeOptional = l2Node.next
                }
            } else {
                // We have no more list 2 values.
                // Append the rest of list 1 to our sorted result, since the list was already sorted &
                // we've already appended any smaller values to the result.
                // Now we set our list 1 pointer to nil to break out of the while loop.
                append(l1Node)
                l1NodeOptional = nil
            }
        }
        
        // This is needed in case we went through all list 1 values and there are still list 2 values.
        // Just append the rest of list 2 since it contains sorted values that come after any values we've appended so far.
        append(l2NodeOptional)
        
        return result
    }
}

Sweet, that will solve the problem. It does seem like a lot of code though, and if you noticed, we’re basically doing the same thing over and over (comparing the first elements of two lists & taking the smaller one). That should have you wondering if we can do the same thing recursively. In this case, using recursion actually reduces the amount of code required by quite a bit! Although recursion often sounds difficult/confusing/scary (believe me, I often feel like that when trying to solve recursive problems), it can be remarkably simple and elegant once you get the hang of it.

In the recursive solution below, we just repeat one step over and over (compare the first node of two lists & take the smaller one). The tricky part is making recursion work. Above all, remember what the function is supposed to do. It returns a sorted list. First we need to handle the base case, which is when we reach the end of either list. If either list has ended, we just return the other (which is a sorted list, so our function does what it’s supposed to in the base case). The next part is to incrementally solve the problem. Since we have two non empty lists, we just need to compare the first node values and select the smaller one. Now that we know the first element in the sorted list, we can recursively call our function to get the rest of the merged list (we need to trust the function to do what it says it does), and then we append the rest of the nodes in sorted order to this first node. We then just return the first/head node in our sorted list & we’re done. Let’s take a look at the code:


class Solution {
    func mergeTwoLists(_ list1: ListNode?, _ list2: ListNode?) -> ListNode? {
        
		// Handle the base case.
		// If a list is empty, return the other list.
		// The other list may be empty as well, but that won't break anything.
		// If we have only one list we can just return it as the sorted list, since the input lists are guaranteed to be sorted.
        guard let list1 = list1 else { return list2 }
        guard let list2 = list2 else { return list1 }

		// This variable will hold the head of our final sorted list
        var result: ListNode? 

		// This is where the surprisingly simple recursive logic comes in.
		// If the first node in list1 should come before list2 (list1.val is less than list2.val),
		// then the head of list1 is the first element (head) of our result.
		// (if list1.val and list2.val are equal then it doesn't matter which comes first, 
		// it's just more clear we're assuming this by using `<=`)
		// Now that we've found the first element in our final result,
		// we need to get the next largest node and point to it.
		// To find the next element, call our function again.
		// Each recursive call will add the next element to the chain,
		// until we end at the base case and the recursion stops.
		// If we forget about recursion for a moment, 
		// it also makes sense that our result will be sorted correctly
		// if we select the node that should come first between list1 and list2, 
		// then append a sorted list to it.
        if list1.val <= list2.val {
            result = list1
            result?.next = mergeTwoLists(list1.next, list2) 
        } else {
            result = list2
            result?.next = mergeTwoLists(list1, list2.next)
        }

		// Result is the head of our sorted list, so we can just return it.
        return result
    }
}

It’s so much shorter! I have to admit I needed to think this one through quite a bit to make sense of how it worked. I often have trouble with the “suspension of disbelief” in recursion problems, and I have to work through it step by step (it can be dizzying though). That’s why I emphasized the function doing what it says it does in every code path (base case & recursive case). Then we can trust the function to do what it says it does & each time the function is called recursively it will work towards the base case. It’s quite beautiful once you have it working!

Let’s wrap it up here. Both solutions have the same complexities - time complexity is O(n) since in the worst case (two lists of equal size) we’ll have to iterate through every single element once in order to append it to the result list. Space complexity is also O(1) because we aren’t creating intermediate values - just re-writing list node pointers.

I hope you feel a little more comfortable with recursion after walking through this one (I know I do!). See you next time.